Fundamentals of Classification by Deep Learning with Tensorflow & Keras
- types of Classification Problems,
- possible label encodings,
- Activation & Loss functions,
- accuracy metrics
If you are ready, let’s get started!
Types of Classification Tasks
In general, there are three main types/categories for Classification Tasks in machine learning:
A. binary classification two target classes.
- Is it a dog in the picture?
- Is it a dog or a cat in the picture?
B. multi-class classification more than two exclusive targets, only one class can be assigned to an input
- Which animal is in the picture: cat, dog, lion, horse?
C. multi-label classification more than two non-exclusive targets, one input can be labeled with multiple target classes.
- Which animals are in the picture: cat, dog, lion, horse?
Types of Label Encoding
In general, we can use different encodings for true (actual) labels (y values) :
a floating number (e.g. in binary classification: 1.0 or 0.0)
- cat → 0.0
- dog → 1.0
one-hot encoding (e.g. in multi-class classification: [0 0 1 0 0])
- cat → [1 0 0 0]
- dog → [0 1 0 0]
- lion → [0 0 1 0]
- horse → [0 0 0 1]
multi-hot encoding (e.g. in multi-label classification: [1 0 1 0 0])
- cat, dog → [1 1 0 0]
- dog → [0 1 0 0]
- cat, lion → [1 0 1 0]
- lion, horse → [0 0 1 1]
- cat, dog, lion, horse → [1 1 1 1]
a vector (array) of integers (e.g. in multi-class classification: [[1], [3]])
- cat → 1
- dog → 2
- lion → 3
- horse → 4
We will cover the all possible encodings in the following examples.
Types of Activation Functions for Classification Tasks
In Keras, there are several Activation Functions. Below I summarize two of them:
- Sigmoid or Logistic Activation Function: Sigmoid function maps any input to an output ranging from 0 to 1. For small values (<-5), the sigmoid returns a value close to zero, and for large values (>5) the result of the function gets close to 1. Sigmoid is equivalent to a 2-element Softmax, where the second element is assumed to be zero. Therefore, sigmoid is mostly used for binary classification.
Example: Assume the last layer of the model is as:
outputs = keras.layers.Dense(1, activation=tf.keras.activations.sigmoid)(x)
(NOTE: You can access the complete code on Colab)
# Let the last layer output vector be:
y_pred_logit = tf.constant([-20, -1.0, 0.0, 1.0, 20], dtype = tf.float32)
print("y_pred_logit:", y_pred_logit.numpy())
# and last layer activation function is sigmoid:
y_pred_prob = tf.keras.activations.sigmoid(y_pred_logit)
print("y_pred:", y_pred_prob.numpy())
print("sum of all the elements in y_pred: ",y_pred_prob.numpy().sum())y_pred_logit: [-20. -1. 0. 1. 20.]
y_pred: [2.0611535e-09 2.6894143e-01 5.0000000e-01 7.3105860e-01 1.0000000e+00]
sum of all the elements in y_pred: 2.5
- Softmax function: Softmax converts a real vector to a vector of categorical probabilities. The elements of the output vector are in range (0, 1) and sum to 1. Each vector is handled independently. Softmax is often used as the activation for the last layer of a classification network because the result could be interpreted as a probability distribution. Therefore, Softmax is mostly used for multi-class or multi-label classification.
For example: Assume the last layer of the model is as:
outputs = keras.layers.Dense(3, activation=tf.keras.activations.softmax)(x)
# Assume last layer output is as:
y_pred_logit = tf.constant([[-20, -1.0, 4.5], [0.0, 1.0, 20]], dtype = tf.float32)
print("y_pred_logit:\n", y_pred_logit.numpy())
# and last layer activation function is softmax:
y_pred_prob = tf.keras.activations.softmax(y_pred_logit)
print("y_pred:", y_pred_prob.numpy())
print("sum of all the elements in each vector in y_pred: ",
y_pred_prob.numpy()[0].sum()," ",
y_pred_prob.numpy()[1].sum())y_pred_logit:
[[-20. -1. 4.5]
[ 0. 1. 20. ]]
y_pred: [[2.2804154e-11 4.0701381e-03 9.9592990e-01]
[2.0611535e-09 5.6027960e-09 1.0000000e+00]]
sum of all the elements in each vector in y_pred: 1.0 1.0
- NONE: If we don’t specify any activation function at the last layer, no activation is applied to the outputs of the layer (ie. “linear” activation: a(x) = x).
An Experimental Model
Assume that
- we have an image
IMG_WIDTH, IMG_HEIGHT = 128 ,128
img_array = np.random.randint(255, size=(IMG_WIDTH, IMG_HEIGHT, 3))
img = Image.fromarray(img_array, 'RGB')
display(img)
2. we have a (very toy) classification model:
def create_Model(number_of_classes, activation_function):
inputs = tf.keras.Input(shape=(IMG_WIDTH, IMG_HEIGHT, 3))
x= tf.keras.layers.Flatten()(inputs)
outputs = tf.keras.layers.Dense(number_of_classes, activation=activation_function)(x)
model = tf.keras.Model(inputs, outputs)
return model3. we have 5 classes
number_of_classes =54. we select an activation function for the last layer
activation_function= tf.keras.activations.softmax5. Let’s see the output of the last layer (model)
toy_model= create_Model(number_of_classes, activation_function)
prediction= toy_model(img_array.reshape(1,IMG_WIDTH, IMG_HEIGHT, 3))
print("prediction shape: ", prediction.shape)
print("prediction value: ", prediction[0].numpy())
print("prediction total value: ", prediction[0].numpy().sum())prediction shape: (1, 5)
prediction value: [0.0000000e+00 0.0000000e+00 4.7775544e-36 9.9774182e-01 2.2582330e-03]
prediction total value: 1.0
PLEASE NOTE THAT The softmax & sigmoid activation functions are the most frequently used ones for classification tasks at the last layer.
Types of Loss Functions for Classification Tasks
In Keras, there are several Loss Functions. Below, I summarized the ones used in Classification tasks:
BinaryCrossentropy: Computes the cross-entropy loss between true labels and predicted labels. We use this cross-entropy loss:
- when there are only two classes (assumed to be 0 and 1). For each sample, there should be a single floating-point value per prediction
- when there are two or more labels with multi-hot encoded labels. For each sample, there should be a single floating-point value per label
CategoricalCrossentropy: Computes the cross-entropy loss between the labels and predictions. We use this cross-entropy loss function:
- when there are two or more label classes. We expect labels to be provided in a one-hot representation. There should be # classes floating point values per sample.
- If you want to provide labels as integers, please use SparseCategoricalCrossentropy loss.
SparseCategoricalCrossentropy: Computes the cross-entropy loss between the labels and predictions. We use this cross-entropy loss function:
- when there are two or more label classes. We expect labels to be provided as integers. There should be # classes floating point values per class for y_pred and a single floating-point value per class for y_true.
- If you want to provide labels using one-hot representation, please use CategoricalCrossentropy loss.
IMPORTANT:
- In Keras, these three Cross-Entropy functions expect two inputs: correct / true /actual labels (y) and predicted labels (y_pred):
- As mentioned above, correct (actual) labels can be encoded floating numbers, one-hot, or an array of integer values.
- However, the predicted labels should be presented as a probability distribution.
- If the predicted labels are not converted to a probability distribution by the last layer of the model (using sigmoid or softmax activation functions), we need to inform these three Cross-Entropy functions by setting their from_logits = True.
- If the parameter from_logits is set True in any cross entropy function, then the function expects ordinary numbers as predicted label values and apply the sigmoid transformation on these predicted label values to convert them into a probability distribution. For details, you can check the
tf.keras.backend.binary_crossentropysource code. The below code is taken from TF source code:
if from_logits: return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output)
- Both, categorical cross-entropy and sparse categorical cross-entropy have the same loss function which we have mentioned above. The only difference is the format of the true labels:
- If correct (actual) labels are one-hot encoded, use categorical_crossentropy. Examples (for a 3-class classification): [1,0,0] , [0,1,0], [0,0,1]
- But if correct (actual) labels are integers, use sparse_categorical_crossentropy. Examples for above 3-class classification problem: [1] , [2], [3]
- The usage entirely depends on how we load our dataset.
- One advantage of using sparse categorical cross-entropy is it saves storage in memory as well as time in computation because it simply uses a single integer for a class, rather than a whole one-hot vector.
A simple example:
y_true= [[1,0, 0, 1,0]]
y_pred = [[-160.15834 -378.0461 -156.47006 399.26843 80.386505]]print("\ny_true {} \ny_pred by None {}".format(y_true, y_pred))
print("binary_crossentropy loss: ",
tf.keras.losses.binary_crossentropy (y_true, y_pred, from_logits=True).numpy())y_pred = sigmoid_predictions
print("\ny_true {} \ny_pred by sigmoid {}".format(y_true, y_pred))
print("binary_crossentropy loss: ", tf.keras.losses.binary_crossentropy(y_true, y_pred).numpy())y_pred = softmax_predictions
print("\ny_true {} \ny_pred by softmax {}".format(y_true, y_pred))
print("binary_crossentropy loss: ", tf.keras.losses.binary_crossentropy(y_true, y_pred).numpy())y_true [[1, 0, 0, 1, 0]]
y_pred by None [[ 76.831665 12.804771 94.58808 165.68713 63.18647 ]]
binary_crossentropy loss: [34.115864] y_true [[1, 0, 0, 1, 0]]
y_pred by sigmoid [[1. 0.99999726 1. 1. 1. ]]
binary_crossentropy loss: [34.115864] y_true [[1, 0, 0, 1, 0]]
y_pred by softmax [[0.0000000e+00 0.0000000e+00 1.3245668e-31 1.0000000e+00 0.0000000e+00]]
binary_crossentropy loss: [3.0849898]
Observations:
- When we use None as the activation function, we need to inform the loss function by setting the parameter
from_logits=True - The same loss is calculated when the activation function is None and Sigmoid! Loss functions apply sigmoid to ordinary outputs automatically.
- Different losses are calculated when the activation function is Sigmoid and Softmax: Which one will you select?
- Be careful about the classification type and true label encoding: In the above example, true label encoding (multi-hot) indicates that the problem is multi-label! Thus we need to use sigmoid as the activation function and binary cross-entropy for the loss function as we discussed above.
Types of Accuracy Metrics
Keras has several accuracy metrics. In classification, we can use the followings:
Accuracy: Calculates how often predictions equal labels.
y_true = [[1], [1], [0], [0]]
y_pred = [[0.99], [1.0], [0.01], [0.0]]
print("Which predictions equal to labels:", np.equal(y_true, y_pred).reshape(-1,))
m = tf.keras.metrics.Accuracy()
m.update_state(y_true, y_pred)
print("Accuracy: ",m.result().numpy())Which predictions equal to labels: [False True False True]
Accuracy: 0.5
Binary Accuracy: Calculates how often predictions match binary labels.
- We mostly use Binary Accuracy for binary classification and multi-label classification if target (true) labels are encoded in one-hot or multi-hot vectors.
- Binary classification example:
y_true = [[1], [1], [0], [0]]
y_pred = [[0.49], [0.51], [0.5], [0.51]]
m = tf.keras.metrics.binary_accuracy(y_true, y_pred, threshold=0.5)
print("Which predictions match with binary labels:", m.numpy())
m = tf.keras.metrics.BinaryAccuracy()
m.update_state(y_true, y_pred)
print("Binary Accuracy: ", m.result().numpy())Which predictions match with binary labels: [0. 1. 1. 0.]
Binary Accuracy: 0.5
- Multi-label classification example:
y_true = [[1, 0, 1], [0, 1, 1]]
y_pred = [[0.52, 0.28, 0.60], [0.40, 0.50, 0.51]]
m = tf.keras.metrics.binary_accuracy(y_true, y_pred, threshold=0.5)
print("Which predictions match with binary labels:", m.numpy())
m = tf.keras.metrics.BinaryAccuracy()
m.update_state(y_true, y_pred)
print("Binary Accuracy: ", m.result().numpy())Which predictions match with binary labels: [1. 0.6666667]
Binary Accuracy: 0.8333334
Categorical Accuracy: Calculates how often predictions match one-hot labels.
- We mostly use Categorical Accuracy in multi-class classification if target (true) labels are encoded in one-hot vectors.
# assume 3 classes exist
y_true = [[ 0, 0, 1], [ 0, 1, 0]]
y_pred = [[0.1, 0.1, 0.8], [0.05, 0.92, 0.3]]
m = tf.keras.metrics.categorical_accuracy(y_true, y_pred)
print("Which predictions match with one-hot labels:", m.numpy())
m = tf.keras.metrics.CategoricalAccuracy()
m.update_state(y_true, y_pred)
print("Categorical Accuracy:", m.result().numpy())Which predictions match with one-hot labels: [1. 1.]
Categorical Accuracy: 1.0
SparseCategorical Accuracy: Calculates how often predictions match integer labels.
- We mostly use SparseCategorical Accuracy for multi-class classifications if target (true) labels are encoded in integer vectors.
# assume 3 classes exist
y_true = [[2], [1],[0]]
y_pred = [[0.1, 0.6, 0.3], [0.05, 0.95, 0], [0.75, 0.25, 0]]
m = tf.keras.metrics.sparse_categorical_accuracy(y_true, y_pred)
print("Which predictions match with one-hot labels:", m.numpy())
m = tf.keras.metrics.SparseCategoricalAccuracy()
m.update_state(y_true, y_pred)
print("Categorical Accuracy:", m.result().numpy())Which predictions match with one-hot labels: [0. 1. 1.]
Categorical Accuracy: 0.6666667
PARTS
Now, after learning all the important components of classification in Deep learning, you can move on to sample classification problems.
In the following parts, we will see how to apply all these functions for solving specific classification problems in detail.
We will observe their effects on the model performance by designing and evaluating a Keras Deep Learning Model on a selected TF Dataset.
You can access all the parts of the Classification tutorial series here.
You can access all these parts on YouTube in ENGLISH or TURKISH
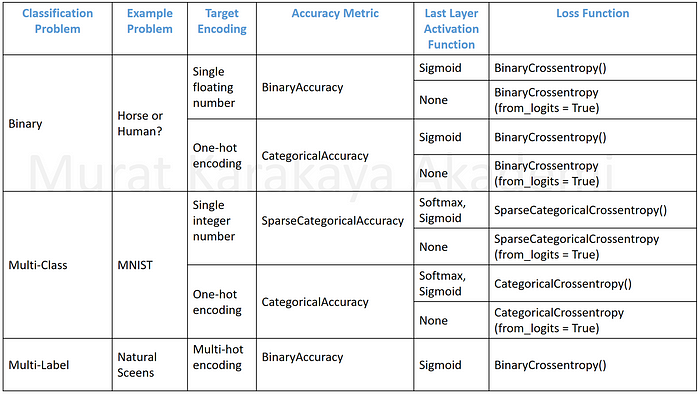
At the end of each part, we will summarize the experiment results in a cheat table and advice on how to use these components.
References
Keras API reference / Losses / Probabilistic losses
Tensorflow Data pipeline (tf.data) guide
How does TensorFlow sparsecategoricalcrossentropy work?
Cross-entropy vs sparse-cross-entropy: when to use one over the other

