SEQ2SEQ LEARNING PART E: Encoder-Decoder for Variable Input And Output Sizes: Padding & Masking

Welcome to Part E of the Seq2Seq Learning Tutorial Series. In this tutorial, we will design an Encoder-Decoder model to handle variable-size input and output sequences by using Padding and Masking methods. We will train the model by using the Teacher Forcing technique which we covered in Part D.

You can access all my SEQ2SEQ Learning videos on Murat Karakaya Akademi Youtube channel in ENGLISH or in TURKISH. You can access all the tutorials in this series from my blog at www.muratkarakaya.net. You can access this Colab Notebook using the link.

If you would like to follow up on Deep Learning tutorials, please subscribe to my YouTube Channel or follow my blog on muratkarakaya.net.

If you are ready, let’s get started!

Photo by Jeffrey Brandjes on Unsplash

REMINDER:

This is the Part E of the Seq2Seq Learning series.
Please check out the previous part to refresh the necessary background knowledge in order to follow this part with ease.

A Simple Seq2Seq Problem: The reversed sequence problem

Assume that:

We are given a parallel data set including X (input) and y (output) such that X[i] and y[i] have some relationship.

In real life (like Machine Language Translation, Image Captioning, etc.), we are given (or build) a parallel dataset: X sequences and corresponding y sequences

We use the parallel data sets to train a seq2seq model which would learn
how to convert/transform an input sequence from X to an output sequence in y
For instance: we are given the same book’s text in English (X) and in Turkish (y). Thus the statement X[i] in English is translated into Turkish as y[i] statement. We use these parallel data sets to train a seq2seq model which would learn how to convert/transform X[i] to y[i]

However, to set up an easily traceable example, I opt out to prepare a rather simple sequence learning problem.

Consider two parallel sequence datasets X and y as below:

X[0]=[3, 2, 9, 4]…………………………….y[0]=[4, 2]

X[1]=[7, 6, 5, 2, 5, 2]…………………….. y[1]=[2, 2, 6]

X[2]=[1, 7, 5, 1, 3]………………………….y[2]=[]

NOTICE THAT input (X) and output (y) sequences have variable lengths

Actually, for this simple Seq2Seq Learning problem, we formulate the y sequence as the even numbers of the given sequence (X) in reverse order.
Assume that you do not know that relation: You only have 2 parallel datasets X and y

In this part, we will develop an encoder-decoder model for the above variable-size input and output sequences

To create parallel datasets X and y, I already prepare a function and an interface to configure it as below

#@title Configure problem

min_timesteps_in =   4
max_timesteps_in =   8

input_dimension = 10   
#each value is one_hot_encoded with 10 0/1



# generate datasets
train_size= 4000 
test_size = 200  

X_train, y_train , X_test, 	y_test=create_dataset(train_size, test_size, min_timesteps_in, max_timesteps_in, input_dimension , verbose=True)Sample X and y sequences (in Raw Format)
X[ 0 ]=[6, 5, 5, 8, 1] ........ y[ 0 ]=[8, 6]
X[ 1 ]=[6, 6, 5, 9, 9, 2, 4] ........ y[ 1 ]=[4, 2, 6, 6]
X[ 2 ]=[2, 3, 1, 8, 1, 9, 4, 2] ........ y[ 2 ]=[2, 4, 8, 2]
X[ 3 ]=[5, 4, 5, 3] ........ y[ 3 ]=[4]
X[ 4 ]=[6, 2, 4, 5, 6] ........ y[ 4 ]=[6, 4, 2, 6]

Each input and output sequences are converted one_hot_encoded format with input_dimension =  10
X[0]=
[[0 0 0 0 0 0 1 0 0 0]
 [0 0 0 0 0 1 0 0 0 0]
 [0 0 0 0 0 1 0 0 0 0]
 [0 0 0 0 0 0 0 0 1 0]
 [0 1 0 0 0 0 0 0 0 0]]
y[0]=
[[0 0 0 0 0 0 0 0 1 0]
 [0 0 0 0 0 0 1 0 0 0]]

Generated sequence datasets as follows [sample_size,time_steps, input_dimension]
X_train.shape:  (4000,) y_train.shape:  (4000,)
X_test.shape:  (200,) y_test.shape:  (200,)
time: 167 ms

IMPORTANT:

Pay attention to the shapes of X and y data sets. Even though we created 3D arrays [sample_size,time_steps, input_dimension], we observed above that Python reports their corresponding shapes as (4000,) or (200,). Why? Because, other than the sample_size dimension, other dimensions do NOT have a fixed size! time_steps and input_dimension have variable sizes! Therefore, Python can NOT print their shapes.
I reserve 0 (zero) as a special symbol and therefore I do NOT use it in sequences as a number!

How to handle variable Input and Output sequence size

In our previous parts, we assumed that the input and output sequence sizes of all samples are fixed and known in advance
Now, we relax this requirement by assuming input & output sequence sizes may vary from sample to sample
However, in Artificial Neural Network models (including encoder-decoder models), the first and last layers have a fixed number of neurons and during training, we need to provide fixed-size samples in the input (X) and output (y) data sets.
Therefore, ANN models should be trained with samples structured in a fixed-size shape.
However, since we have variable-size input/output samples, we need to convert them into a fixed-size shape.
The popular solution has two parts:
During training: we will use padding and masking to make all sample sequence sizes equal.
During inference: For variable output sequence size, we will modify the decoder such that it will work in a loop and stop generating output when a condition is met. This condition can be in two ways:
If the decoder generated the maximum number of outputs defined by the user, or
If the decoder generated a special “STOP” symbol

Don’t worry, we will implement the above solution step by step.

So let’s get started!

#Padding

Padding means appending a special symbol to the beginning or end of a sequence
The special symbol is mostly 0 (zero) but can be any symbol that is not used as a value in the sequences
We will use padding to extend the given sequence to a specific size
Assume we are given the sequence [4, 6, 8], we can pad two 0 (zeros) in two different ways:
post-padding: We append the padding at the end of the sequence such that the resulting sequence becomes [4, 6, 8, 0, 0]
pre-padding: We can also append the padding to the beginning of the sequence: [0, 0, 4, 6, 8]
Notice that: Even the original information ([4, 6, 8]) is reserved, the size of the padded sequence ([4, 6, 8, 0, 0] or [0, 0, 4, 6, 8] ) is changed/incremented to 5 instead of 3!
Important: Tensorflow/Keras recommends using “post” padding when working with RNN layers in order to be able to use the CuDNN implementation of the layers. Thus, we will use post-padding in this tutorial.

How to use padding in variable-size input/output sequences?

First, we will find out the maximum number of time steps in input/output data sets
Then, we will append the necessary number of paddings to the end of each sequence such that their number of time steps will be equal to the maximum number of time steps in the data set.
In the end, all the input/output sequences will have the same number of time steps

What would be the effect of padding in training & testing

Remember that we had reserved 0 (zero) when we created the X and y datasets
We reserved 0 (zero) for padding

In training

the encoder will consume all the sequence and the paddings
the decoder will learn to produce 0 (zero) when the output sequence finishes

In testing

the encoder will consume all the sequence and the paddings
the decoder will stop predicting
when it generates the “STOP” symbol (0 zero) as output, or
when it exceeds the number of maximum outputs defined by the user

Let’s apply paddings to input/output sequences

First, we will find out the maximum sequence size for input/output sequences in the Train data set:

max_input_sequence= max(len(seq) for seq in X_train)
max_output_sequence= max(len(seq) for seq in y_train)

print('max_input_sequence: ', max_input_sequence)
print('max_output_sequence: ', max_output_sequence)max_input_sequence:  8
max_output_sequence:  8
time: 4.01 ms

In this example, max_input_sequence and max_ouput_sequence are equal but they could be different for your datasets. The point is you need to handle input and output sequences separately!

Then, we will append the necessary number of paddings to the end of each input sequence such that their number of time steps will be equal to the maximum number of time steps in the data set.

We can use pad_sequences() function from Keras preprocessing library as below.

pad_sequences(sequences, maxlen=None, dtype='int32', padding='pre', truncating='pre', value=0.0)

Note that:

If the maxlen argument is NOT provided, the function automatically sets maxlen to the maximum sequence size in the samples. However, for the sake of clarity, I will provide max_input_sequence and max_ouput_sequence to the pad_sequences() function.
I will provide the masking value as [1, 0, 0, 0, 0, 0, 0, 0, 0, 0] which is the one-hot-encoded representation of 0 (zero) padding!

from keras.preprocessing.sequence import pad_sequences
X_train_padded = pad_sequences(X_train, maxlen= max_input_sequence, padding='post', value=[1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
print("X_train shape: ",X_train.shape)
print("X_train_padded shape: ",X_train_padded.shape)

y_train_padded = pad_sequences(y_train, maxlen= max_output_sequence, padding='post', value=[1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
print("y_train shape: ",y_train.shape)
print("y_train_padded shape: ",y_train_padded.shape)X_train shape:  (4000,)
X_train_padded shape:  (4000, 8, 10)
y_train shape:  (4000,)
y_train_padded shape:  (4000, 8, 10)
time: 49.9 ms

Important: After padding, each sequence in X_train_padded has the same shape: (4000, 8, 10): 8 time-steps with a 10-dimension representation! That is, we have fixed-size input data set!

Let’s see an example input before and after padding:

i=0
print("____Sample Input (Raw Format)____")
print("Original:\n", one_hot_decode(X_train[i]))
print("Padded:\n",one_hot_decode(X_train_padded[i]))
print("____Corresponding Output (Raw Format)____")
print("Original:\n", one_hot_decode(y_train[i]))
print("Padded:\n",one_hot_decode(y_train_padded[i]))____Sample Input (Raw Format)____
Original:
 [6, 5, 5, 8, 1]
Padded:
 [6, 5, 5, 8, 1, 0, 0, 0]
____Corresponding Output (Raw Format)____
Original:
 [8, 6]
Padded:
 [8, 6, 0, 0, 0, 0, 0, 0]
time: 4.09 ms

Let’s apply padding to the Test data set as well

X_test_padded = pad_sequences(X_test, maxlen= max_input_sequence, padding='post', value=[1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
print("X_test shape: ",X_test.shape)
print("X_test_padded shape: ",X_test_padded.shape)

y_test_padded = pad_sequences(y_test, maxlen= max_output_sequence, padding='post', value=[1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
print("y_test shape: ",y_test.shape)
print("y_test_padded shape: ",y_test_padded.shape)X_test shape:  (200,)
X_test_padded shape:  (200, 8, 10)
y_test shape:  (200,)
y_test_padded shape:  (200, 8, 10)
time: 13 ms

Masking

Masking is a way to tell sequence-processing layers that certain timesteps in the input are missing, and thus should be skipped when processing the data.
Above we applied padding and all samples have a uniform sequence length.
Now, we need to inform the model that some part of the data is actually padding and should be ignored during processing.
That mechanism is called “masking”.
There are three ways to introduce input masks in Keras models:

Add a keras.layers.Masking layer.
Configure a keras.layers.Embedding layer with mask_zero=True.
Pass a mask argument manually when calling layers that support this argument (e.g. RNN layers).

In this tutorial, I will use the Masking layer. As you remember, we padded the sequences with 0 (zero) value. However, the 0 value is converted to one-hot encoding. Thus, the mask value is the one-hot-encoded representation of 0 (zero) which is [1 0 0 0 0 0 0 0 0 0]

Therefore, we will create a Masking layer as below:

masking = tf.keras.layers.Masking(mask_value= [1, 0, 0, 0, 0, 0, 0, 0, 0, 0])

Encoder-Decoder model with Teacher Forcing

I assume that you have already studied the previous parts and you have got familiar with the Encoder-Decoder model with Teacher Forcing.

If you have not, please review at least Part D before continue.

A QUICK REMINDER: HOW TO TRAIN AN ENCODER — DECODER WITH TEACHER FORCING

The generic steps are as follows:

The decoder produces the output sequence one by one
For each output, the decoder consumes a context vector and an input
The initial context vector is created by the encoder
The initial input is a special symbol for the decoder to make it start, e.g. ‘start’
Using initial context and initial input, the decoder will generate the first output

However, the input to the decoder during the loop is different

For the next output,
the decoder will use its current state as the context vector
we (the teacher!) provide the correct output to the decoder as input
The decoder will work in such a loop using its state and the provided correct output as the next step context vector and input until the generated output is a special symbol ‘stop’ or the pre-defined maximum steps (length of output) is reached.

Therefore, we need to provide 2 input sequence TRAIN AN ENCODER — DECODER WITH TEACHER FORCING such that

input to encoder: [4 7 2 0 0 0 0 0]
input to decoder: [0 2 4 0 0 0 0 0]

Note that:

The expected output is [2 4 0 0 0 0 0 0] — — even numbers in reverse order of input to the encoder
0 (zero) is selected as a special symbol for ‘start’ and ‘padding’
input to decoder is created by shifting the expected output by one time steps and adding a ‘start’ token as the first token: [2 4 0 0 0 0 0 0] — — → [0 2 4 0 0 0 0 0]
At the first cycle, the decoder will use the encoder’s state and its first input which is 0 ([1 0 0 0 0 0 0 0] ) from [0 2 4 0 0 0 0 0] to generate the first expected output which is 2 from [2 4 0 0 0 0 0 0]
Assume that the decoder predicts 5
in the generic Encoder-Decoder model, the decoder will use 5 to generate/predict the next token
in teacher forcing, we (the teacher!) provide the second input from [0 2 4 0 0 0 0 0] which is 2 to the decoder to generate/predict the next token

Thus, during training, the teacher enforces the decoder to condition itself to generate/predict the next token according to the given correct input!

HOW TO USE AN ENCODER—DECODER MODEL TRAINED WITH TEACHER FORCING FOR INFERENCE (PREDICTION)

We need 2 input sequences:

Input for encoder: encoder_inputs
Input for decoder: decoder_inputs

The encoder_inputs is given
However, this time we do not have the correct outputs
Therefore, we will provide the predicted output as the input.
The first input is ‘start’ and the other inputs will be the outputs from the previous cycle

PREPARE TRAINING DATA SETS

To train the Encoder-Decoder model we need to work on the train data set such that we will prepare 3 data sets:

Input for the encoder (encoder_inputs): training input data (X)
Input for the decoder (decoder_inputs): shifted and appended START output data (y)
The target for the decoder (decoder_target_data): output data (y)

#Prepare TRAIN data set
encoder_input_data = X_train_padded.copy()
decoder_target_data = y_train_padded.copy()
decoder_input_data = decoder_target_data.copy()
for i, samples in enumerate(decoder_target_data):
  seq = one_hot_decode(samples)
  shifted= shift(seq, 1, cval=0)
  decoder_input_data[i]=one_hot_encode(shifted,input_dimension)
print("Data for Train")
print('encoder_input_data (X): ', one_hot_decode(encoder_input_data[1]))
print('decoder_input_data (teacher forcing): ',one_hot_decode(decoder_input_data[1]))
print('decoder_target_data (y):',one_hot_decode(decoder_target_data[1]))
print(encoder_input_data.shape)

#Prepare TEST data set
encoder_input_test = X_test_padded.copy()
decoder_target_test = y_test_padded.copy()
decoder_input_test= decoder_target_test.copy()
for i, samples in enumerate(decoder_target_test):
  seq = one_hot_decode(samples)
  shifted= shift(seq, 1, cval=0)
  decoder_input_test[i]=one_hot_encode(shifted,input_dimension)Data for Train
encoder_input_data (X):  [6, 6, 5, 9, 9, 2, 4, 0]
decoder_input_data (teacher forcing):  [0, 4, 2, 6, 6, 0, 0, 0]
decoder_target_data (y): [4, 2, 6, 6, 0, 0, 0, 0]
(4000, 8, 10)
time: 365 ms

CREATE AN ENCODER—DECODER MODEL WITH TEACHER FORCING TO TRAIN

Define the model that will turn encoder_input_data & decoder_input_data into decoder_target_data
complete the decoder model by adding a Dense layer with Softmax activation function for prediction of the next output
The dense layer will output one-hot encoded representation as we did for the input
Therefore, we will use the input_dimension number of neurons

#@title LSTMoutputDimension
LSTMoutputDimension = 32 #@param {type:"integer"}time: 1.04 ms# Define an input sequence and process it.
encoder_inputs= Input(shape=(max_input_sequence, input_dimension), name='encoder_inputs')

masking = tf.keras.layers.Masking(mask_value= [1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
encoder_inputs_masked = masking(encoder_inputs)
encoder_inputs_masked = encoder_inputs

encoder_lstm=LSTM(LSTMoutputDimension, return_state=True, name='encoder_lstm')
LSTM_outputs, state_h, state_c = encoder_lstm(encoder_inputs_masked)


# We discard `LSTM_outputs` and only keep the other states.
encoder_states = [state_h, state_c]



decoder_inputs = Input(shape=(None, input_dimension), name='decoder_inputs')
decoder_lstm = LSTM(LSTMoutputDimension, return_sequences=True, return_state=True, name='decoder_lstm')

# Set up the decoder, using `context vector` as initial state.
decoder_outputs, _, _ = decoder_lstm(decoder_inputs,
                                     initial_state=encoder_states)

#complete the decoder model by adding a Dense layer with Softmax activation function 
#for prediction of the next output
#Dense layer will output one-hot encoded representation as we did for input
#Therefore, we will use input_dimension number of neurons
decoder_dense = Dense(input_dimension, activation='softmax', name='decoder_dense')
decoder_outputs = decoder_dense(decoder_outputs)

# put together
model_encoder_training = Model([encoder_inputs, decoder_inputs], decoder_outputs, name='model_encoder_training')time: 510 ms

compile the model

model_encoder_training.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model_encoder_training.summary()
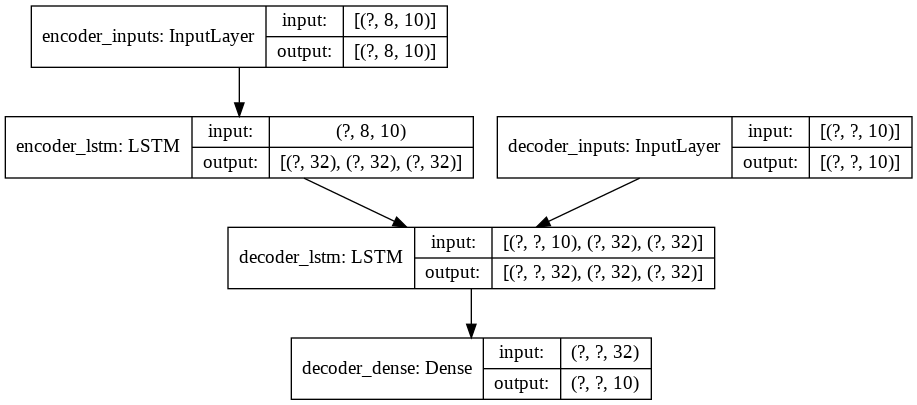
plot_model(model_encoder_training, show_shapes=True)Model: "model_encoder_training"
__________________________________________________________________________________________________
Layer (type)                    Output Shape         Param #     Connected to                     
==================================================================================================
encoder_inputs (InputLayer)     [(None, 8, 10)]      0                                            
__________________________________________________________________________________________________
decoder_inputs (InputLayer)     [(None, None, 10)]   0                                            
__________________________________________________________________________________________________
encoder_lstm (LSTM)             [(None, 32), (None,  5504        encoder_inputs[0][0]             
__________________________________________________________________________________________________
decoder_lstm (LSTM)             [(None, None, 32), ( 5504        decoder_inputs[0][0]             
                                                                 encoder_lstm[0][1]               
                                                                 encoder_lstm[0][2]               
__________________________________________________________________________________________________
decoder_dense (Dense)           (None, None, 10)     330         decoder_lstm[0][0]               
==================================================================================================
Total params: 11,338
Trainable params: 11,338
Non-trainable params: 0
__________________________________________________________________________________________________

We train the model while monitoring the loss on a held-out set of 20% of the samples as below.
However, I prepared a custom train_test function for getting a detailed report of training and testing.

# Run training
model_encoder_training.fit([encoder_input_data, decoder_input_data], decoder_target_data,
          batch_size=32,
          epochs=50,
          validation_split=0.2)train_test(model_encoder_training, [encoder_input_data, decoder_input_data], decoder_target_data ,
           [encoder_input_test, decoder_input_test], 
           decoder_target_test, epochs=50, batch_size=64, patience=3,verbose=2)training for  50  epochs begins with EarlyStopping(monitor= val_loss, patience= 3 )....
Epoch 1/50
57/57 - 1s - loss: 1.4561 - accuracy: 0.6564 - val_loss: 0.9325 - val_accuracy: 0.6622
. . .. . Epoch 48/50
57/57 - 0s - loss: 0.0113 - accuracy: 0.9992 - val_loss: 0.0145 - val_accuracy: 0.9981
Epoch 49/50
57/57 - 0s - loss: 0.0109 - accuracy: 0.9992 - val_loss: 0.0122 - val_accuracy: 0.9991
Epoch 50/50
57/57 - 0s - loss: 0.0117 - accuracy: 0.9986 - val_loss: 0.0212 - val_accuracy: 0.9959
50  epoch training finished...

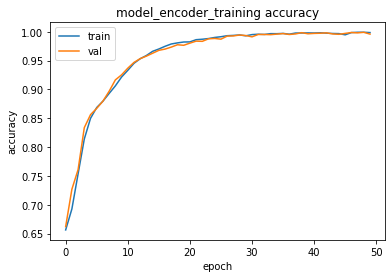
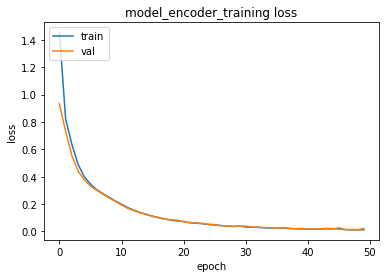
PREDICTION ACCURACY (%):
Train: 99.581, Test: 99.500

10 examples from test data...
Input                      Expected                   Predicted                     T/F
[7, 1, 1, 2, 0, 0, 0, 0]   [2, 0, 0, 0, 0, 0, 0, 0]   [2, 0, 0, 0, 0, 0, 0, 0]   True
[2, 5, 7, 7, 9, 0, 0, 0]   [2, 0, 0, 0, 0, 0, 0, 0]   [2, 0, 0, 0, 0, 0, 0, 0]   True
[9, 1, 1, 4, 5, 5, 0, 0]   [4, 0, 0, 0, 0, 0, 0, 0]   [4, 0, 0, 0, 0, 0, 0, 0]   True
[1, 7, 2, 4, 1, 6, 2, 3]   [2, 6, 4, 2, 0, 0, 0, 0]   [2, 6, 4, 2, 0, 0, 0, 0]   True
[8, 8, 8, 3, 4, 2, 2, 1]   [2, 2, 4, 8, 8, 8, 0, 0]   [2, 2, 4, 8, 8, 8, 0, 0]   True
[4, 3, 4, 4, 1, 1, 8, 0]   [8, 4, 4, 4, 0, 0, 0, 0]   [8, 4, 4, 4, 0, 0, 0, 0]   True
[4, 3, 6, 4, 3, 0, 0, 0]   [4, 6, 4, 0, 0, 0, 0, 0]   [4, 6, 4, 0, 0, 0, 0, 0]   True
[6, 9, 2, 6, 6, 9, 7, 0]   [6, 6, 2, 6, 0, 0, 0, 0]   [6, 6, 2, 6, 0, 0, 0, 0]   True
[5, 6, 7, 3, 4, 4, 2, 8]   [8, 2, 4, 4, 6, 0, 0, 0]   [8, 2, 4, 4, 6, 0, 0, 0]   True
[9, 9, 1, 2, 1, 6, 4, 6]   [6, 4, 6, 2, 0, 0, 0, 0]   [6, 4, 6, 2, 0, 0, 0, 0]   True
Accuracy:  1.0
time: 27.7 s

IMPORTANT:

The above model is ONLY for Training. WHY?

Because:

Teacher Forcing needs to know the correct output beforehand
Teacher Forcing is a method for improving the training process
The model employing Teacher Forcing CAN NOT BE USED in inference/testing

Therefore,

The model that we trained above CAN NOT BE DIRECTLY USED in Inference/Testing
We will use some layers (with their weights) of the trained model to create a new model
The new model will not use Teacher Learning
Thus, the input to the new model will NOT BE [encoder_input_data, decoder_input_data] as the way we designed in model_encoder_training

Remember:

In Teacher Forcing, we set decoder_input_data such that it begins with a special symbol start and continues with the target sequence data except for the last time step.

Now, during inference (testing), we do not know the correct (expected) target data beforehand!
We define the decoder_input_data as follows:
it begins with a special symbol start
it will continue with an input created by the decoder at the previous time step
in other words, the decoder’s output at time step t will be used decoder’s input at time step t+1

Encoder-Decoder Model for Inference

IMPORTANT:

We create a separate encoder model by using the trained layers in the above model. For example, in the following model, we will use encoder_inputs, encoder_states for encoding which are parts of the encoder model, we trained above. That is, these layers come with its** trained weights** with Teacher Forcing

encoder_model = Model(encoder_inputs, encoder_states)time: 10.1 ms

Then we create a separate decoder model by using the trained layers in the above model

then design the decoder model by defining layers for:
inputs
decoding (LSTM)
outputs

IMPORTANT: pay attention that in this model we use decoder_lstm for decoding which is a part of the decoder model, we trained above. That is this layer comes with its trained weights with Teacher Forcing

decoder_state_input_h = Input(shape=(LSTMoutputDimension,))
decoder_state_input_c = Input(shape=(LSTMoutputDimension,))
decoder_states_inputs = [decoder_state_input_h, decoder_state_input_c]

decoder_outputs, state_h, state_c = decoder_lstm(
    decoder_inputs, initial_state=decoder_states_inputs)
decoder_states = [state_h, state_c]
decoder_outputs = decoder_dense(decoder_outputs)
decoder_model = Model(
    [decoder_inputs] + decoder_states_inputs,
    [decoder_outputs] + decoder_states)time: 244 ms

Even though we define the encoder and decoder models we still need to dynamically provide the decoder_input_data as follows:
it begins with a special symbol start
it will continue with an input created by the decoder at the previous time step
in other words, the decoder’s output at time step t will be used decoder’s input at time step t+1

Let’s code the Encoder-Decoder model for Inference as a function

def decode_sequence(input_seq):
    # Encode the input as state vectors.
    states_value = encoder_model.predict(input_seq)

    # Generate empty target sequence of length 1.
    target_seq = np.zeros((1, 1, input_dimension))
    # Populate the first character of target sequence with the start character.
    target_seq[0, 0, 0] = 1

    # Sampling loop for a batch of sequences
    # (to simplify, here we assume a batch of size 1).
    stop_condition = False
    decoded_seq = list()
    while not stop_condition:

        # in a loop
        # decode the input to a token/output prediction + required states for context vector
        output_tokens, h, c = decoder_model.predict(
            [target_seq] + states_value)

        # convert the token/output prediction to a token/output
        sampled_token_index = np.argmax(output_tokens[0, -1, :])
        sampled_char = sampled_token_index
        # add the predicted token/output to output sequence
        decoded_seq.append(sampled_char)
        

        # Exit condition: either hit max length
        # or find stop character.
        if (sampled_char == 0 or
           len(decoded_seq) == max_output_sequence):
            stop_condition = True

        # Update the input target sequence (of length 1) 
        # with the predicted token/output 
        target_seq = np.zeros((1, 1, input_dimension))
        target_seq[0, 0, sampled_token_index] = 1.

        # Update input states (context vector) 
        # with the ouputed states
        states_value = [h, c]

        # loop back.....
        
    # when loop exists return the output sequence
    return decoded_seqtime: 21 ms

Let’s call the function above for inference as below.

IMPORTANT: Since we used the trained layers here, we do NOT need to train recently created models.

print('Input \t\t\t\t\t  Expected  \t\t\t   Predicted \t\tT/F')
correct =0 
sampleNo =  50
for sample in range(0,sampleNo):
  predicted= decode_sequence(encoder_input_data[sample].reshape(1,max_input_sequence,input_dimension))
  if (one_hot_decode(decoder_target_data[sample])== predicted+ [0] * (max_output_sequence- len(predicted))):
    correct+=1
  print( one_hot_decode(encoder_input_data[sample]), '\t\t', 
        one_hot_decode(decoder_target_data[sample]),'\t', predicted,
        '\t\t',one_hot_decode(decoder_target_data[sample])== predicted+ [0] * (max_output_sequence- len(predicted)))
print('Accuracy: ', correct/sampleNo)Input 					  Expected  			   Predicted 		T/F
[6, 5, 5, 8, 1, 0, 0, 0] 		 [8, 6, 0, 0, 0, 0, 0, 0] 	 [8, 6, 0] 		 True
[6, 6, 5, 9, 9, 2, 4, 0] 		 [4, 2, 6, 6, 0, 0, 0, 0] 	 [4, 2, 6, 6, 0] 		 True
[2, 3, 1, 8, 1, 9, 4, 2] 		 [2, 4, 8, 2, 0, 0, 0, 0] 	 [2, 4, 8, 2, 0] 		 True
[5, 4, 5, 3, 0, 0, 0, 0] 		 [4, 0, 0, 0, 0, 0, 0, 0] 	 [4, 0] 		 True
[6, 2, 4, 5, 6, 0, 0, 0] 		 [6, 4, 2, 6, 0, 0, 0, 0] 	 [6, 4, 2, 6, 0] 		 True
[7, 7, 5, 1, 6, 4, 4, 8] 		 [8, 4, 4, 6, 0, 0, 0, 0] 	 [8, 4, 4, 6, 0] 		 True
[7, 5, 1, 5, 6, 0, 0, 0] 		 [6, 0, 0, 0, 0, 0, 0, 0] 	 [6, 0] 		 True
[9, 4, 5, 3, 2, 9, 0, 0] 		 [2, 4, 0, 0, 0, 0, 0, 0] 	 [2, 4, 0] 		 True
[5, 4, 8, 9, 9, 5, 4, 7] 		 [4, 8, 4, 0, 0, 0, 0, 0] 	 [4, 8, 4, 0] 		 True
[6, 7, 7, 6, 5, 7, 4, 8] 		 [8, 4, 6, 6, 0, 0, 0, 0] 	 [8, 4, 6, 6, 0] 		 True
[3, 4, 4, 7, 9, 8, 8, 0] 		 [8, 8, 4, 4, 0, 0, 0, 0] 	 [8, 8, 4, 4, 0] 		 True
[8, 9, 7, 5, 6, 0, 0, 0] 		 [6, 8, 0, 0, 0, 0, 0, 0] 	 [6, 8, 0] 		 True
[5, 8, 4, 7, 0, 0, 0, 0] 		 [4, 8, 0, 0, 0, 0, 0, 0] 	 [4, 8, 0] 		 True
[3, 9, 1, 9, 0, 0, 0, 0] 		 [0, 0, 0, 0, 0, 0, 0, 0] 	 [0] 		 True
[1, 8, 3, 8, 2, 0, 0, 0] 		 [2, 8, 8, 0, 0, 0, 0, 0] 	 [2, 8, 8, 0] 		 True
[7, 1, 1, 1, 5, 8, 4, 6] 		 [6, 4, 8, 0, 0, 0, 0, 0] 	 [6, 4, 8, 0] 		 True
[9, 8, 8, 7, 0, 0, 0, 0] 		 [8, 8, 0, 0, 0, 0, 0, 0] 	 [8, 8, 0] 		 True
[8, 4, 1, 6, 5, 7, 2, 0] 		 [2, 6, 4, 8, 0, 0, 0, 0] 	 [2, 6, 4, 8, 0] 		 True
[1, 7, 5, 3, 2, 3, 7, 0] 		 [2, 0, 0, 0, 0, 0, 0, 0] 	 [2, 0] 		 True
[3, 2, 8, 8, 2, 0, 0, 0] 		 [2, 8, 8, 2, 0, 0, 0, 0] 	 [2, 8, 8, 2, 0] 		 True
[4, 9, 1, 1, 2, 1, 0, 0] 		 [2, 4, 0, 0, 0, 0, 0, 0] 	 [2, 4, 0] 		 True
[1, 4, 5, 6, 4, 0, 0, 0] 		 [4, 6, 4, 0, 0, 0, 0, 0] 	 [4, 6, 4, 0] 		 True
[2, 9, 3, 4, 1, 5, 5, 3] 		 [4, 2, 0, 0, 0, 0, 0, 0] 	 [4, 2, 0] 		 True
[8, 3, 4, 8, 6, 0, 0, 0] 		 [6, 8, 4, 8, 0, 0, 0, 0] 	 [6, 8, 4, 6, 0] 		 False
[5, 6, 6, 4, 8, 0, 0, 0] 		 [8, 4, 6, 6, 0, 0, 0, 0] 	 [8, 4, 6, 6, 0] 		 True
[9, 1, 3, 1, 0, 0, 0, 0] 		 [0, 0, 0, 0, 0, 0, 0, 0] 	 [0] 		 True
[2, 3, 9, 8, 4, 9, 9, 0] 		 [4, 8, 2, 0, 0, 0, 0, 0] 	 [4, 8, 2, 0] 		 True
[5, 4, 7, 6, 0, 0, 0, 0] 		 [6, 4, 0, 0, 0, 0, 0, 0] 	 [6, 4, 0] 		 True
[1, 7, 5, 2, 4, 9, 0, 0] 		 [4, 2, 0, 0, 0, 0, 0, 0] 	 [4, 2, 0] 		 True
[3, 7, 7, 9, 0, 0, 0, 0] 		 [0, 0, 0, 0, 0, 0, 0, 0] 	 [0] 		 True
[7, 9, 1, 6, 4, 0, 0, 0] 		 [4, 6, 0, 0, 0, 0, 0, 0] 	 [4, 6, 0] 		 True
[4, 1, 1, 3, 6, 0, 0, 0] 		 [6, 4, 0, 0, 0, 0, 0, 0] 	 [6, 4, 0] 		 True
[4, 2, 7, 7, 0, 0, 0, 0] 		 [2, 4, 0, 0, 0, 0, 0, 0] 	 [2, 4, 0] 		 True
[9, 9, 1, 7, 5, 3, 8, 3] 		 [8, 0, 0, 0, 0, 0, 0, 0] 	 [8, 0] 		 True
[8, 5, 2, 8, 7, 8, 0, 0] 		 [8, 8, 2, 8, 0, 0, 0, 0] 	 [8, 8, 2, 8, 0] 		 True
[2, 7, 7, 7, 6, 7, 6, 7] 		 [6, 6, 2, 0, 0, 0, 0, 0] 	 [6, 6, 2, 0] 		 True
[9, 1, 9, 3, 5, 8, 3, 0] 		 [8, 0, 0, 0, 0, 0, 0, 0] 	 [8, 0] 		 True
[1, 3, 3, 9, 3, 0, 0, 0] 		 [0, 0, 0, 0, 0, 0, 0, 0] 	 [0] 		 True
[5, 9, 7, 8, 7, 7, 4, 0] 		 [4, 8, 0, 0, 0, 0, 0, 0] 	 [4, 8, 0] 		 True
[7, 3, 3, 9, 9, 7, 0, 0] 		 [0, 0, 0, 0, 0, 0, 0, 0] 	 [0] 		 True
[4, 3, 5, 8, 0, 0, 0, 0] 		 [8, 4, 0, 0, 0, 0, 0, 0] 	 [8, 4, 0] 		 True
[4, 5, 3, 6, 7, 6, 9, 0] 		 [6, 6, 4, 0, 0, 0, 0, 0] 	 [6, 6, 4, 0] 		 True
[7, 5, 3, 5, 4, 1, 3, 6] 		 [6, 4, 0, 0, 0, 0, 0, 0] 	 [6, 4, 0] 		 True
[3, 4, 1, 4, 8, 2, 3, 0] 		 [2, 8, 4, 4, 0, 0, 0, 0] 	 [2, 8, 4, 4, 0] 		 True
[2, 2, 3, 4, 8, 8, 3, 3] 		 [8, 8, 4, 2, 2, 0, 0, 0] 	 [8, 8, 4, 2, 2, 0] 		 True
[6, 7, 3, 9, 3, 0, 0, 0] 		 [6, 0, 0, 0, 0, 0, 0, 0] 	 [6, 0] 		 True
[8, 3, 3, 8, 0, 0, 0, 0] 		 [8, 8, 0, 0, 0, 0, 0, 0] 	 [8, 8, 0] 		 True
[2, 2, 7, 6, 4, 8, 0, 0] 		 [8, 4, 6, 2, 2, 0, 0, 0] 	 [8, 4, 6, 2, 2, 0] 		 True
[3, 6, 7, 9, 8, 3, 0, 0] 		 [8, 6, 0, 0, 0, 0, 0, 0] 	 [8, 6, 0] 		 True
[1, 7, 2, 7, 9, 6, 7, 0] 		 [6, 2, 0, 0, 0, 0, 0, 0] 	 [6, 2, 0] 		 True
Accuracy:  0.98
time: 10.3 s

Notice that: Decoder stops whenever it generates 0 (zero)

Observations:

Data set (X or y) can have samples whose lengths (time steps) can be different (variable)
We use padding for appending a special symbol to sequences.
We can pad as many as needed for a sequence to make its length equal to the maximum length in the data set.
We use masking to tell the layer to skip these time steps since they hold padding values.
Teacher Forcing is a method to train encoder-decoder models in the Seq2Seq model to accelerate training
Teacher Forcing can ONLY be used at Training
We need to handle how to use the model in inference

References:

Blogs:

Tensorflow/Keras Masking Padding official website
Tensorflow/Keras LSTM official website
A ten-minute introduction to sequence-to-sequence learning in Keras by Francois Chollet
How to Develop an Encoder-Decoder Model with Attention in Keras by Jason Brownlee
Presentations:
LSTM from a programmer’s perspective by Murat Karakaya Akademi
Videos:
LSTM from scratch by Murat Karakaya Akademi
Notebooks:
LSTM intro by Murat Karakaya Akademi
Recap LSTM outputs by Murat Karakaya Akademi

You can follow me on these social networks:

Thursday, November 10, 2022